ＲでＯＲ：日程計画(PERT)

PERT計算
PERT計算用パッケージプログラム
確率PERT計算

日程計画、ＰＥＲＴ計算

新製品の開発、大規模施設の建設、イベントの開催など、大規模プロジェクトの計画作業を効率よく遂行するための強力な道具として「PERT(Project Evaluation and Review Technique)」がある。プロジェクト全体を、まとまりの良い部分作業に分け、各部分作業の所要時間の見積もりと、各作業間の先行後続関係が分かれば、プロジェクトが完了するまでの所要最短時間を見積もり、それを達成するための各部分作業の開始時刻、終了時刻、余裕時間などを計算することが出来る。

PERTというと、先ずアローダイアグラムというネットワーク図を描くことから始めるのが普通、しかし、アローダイアグラムはコミュニケーションの道具としては有効なものの、部分作業が数百を終える大きなプロジェクトになると、アローダイアグラムが描けたとしても見通しが悪いのであまり有効ではない。PERTの有効性は、各作業の作業見積もり時間と作業間の先行後続関係が与えられるだけでプロジェクトの最短所要時間とか、各作業の開始時刻、余裕時間などが計算できることにある。

最早開始時刻、最短所要時間

プロジェクトはいくつかの部分作業（工程）からなり、それらの中には着手の順番（先行、後続関係）が決められているものがある。部分作業を単に「作業」という。作業には見積もり所要時間が与えられている。

先行作業の無い作業は時刻０に開始するものとし、各作業は着手可能になったら直ちに開始するものとすれば、すべての作業が終了した時刻が、プロジェクトの最短所要時間となることは明らかである。それを系統的に計算する手順を説明する。

ある作業の最早開始時刻(earliest start time, ES)とは、その作業が開始できる最も早い時刻のことで、その作業開始に必要な先行作業すべてが予定通り遂行された場合に達成される。最早開始時刻に、その作業の作業時間を足したものを最早終了時刻(earliest finish time, EF)と言う。また、説明を簡単にするために、先行作業のない部分作業の先行作業として、プロジェクト開始のための準備作業（お祓いのようなもの）、後続作業のない部分作業の後続作業として、プロジェクト終了のための確認作業（打ち上げのようなもの）の二つの部分作業を追加する。これらの作業の所要時間は０とする。

プロジェクトの最短所要時間は次のようにして計算する。そのために、まず、すべての作業の最早開始時刻、最早終了時刻を計算する。

「準備」作業の最早開始時刻と最早終了時刻を０とする。
最早終了時刻が計算された作業だけを直接の先行作業とする作業の最早開始時刻を、すべての先行作業の最早終了時刻の最大値とし、それに作業時間を加えて最早終了時刻とする。

このアルゴリズムにより、すべての作業の最早開始時刻が求められるが、このとき、作業の先行後続関係は指定された通りになっているので、「後始末」作業の最早開始時刻までにプロジェクトは完了しているはず。さらに、先行後続の最早開始時刻、最早終了時刻を子細に観察すると、次のようなことが分かる。

ある作業Ａの最早開始時刻は、その作業のすべての先行作業の最早終了時刻の最大値だから、それら先行作業の中の少なくとも一つの作業Ｂで、その最早終了時刻が作業Ａの最早開始時刻に等しいものがあるはず。同様な考察により、作業Ｂの先行作業の中から、その最早終了時刻が作業Ｂの最早開始時刻に等しいものが見つかる。この手順を繰り返すと、「後始末」作業から順に遡って、有限回のステップで「準備」作業に到達する。その結果、「準備」作業を先行作業とする作業から始めて、「後始末」作業まで、最早開始時刻がその先行作業の最早終了時刻に等しくなっているという作業列を見つけることが出来る。この一連の作業列は、先行後続の関係にあり、同時に実施することは出来ない。また「後始末」作業の最早開始時刻まで、必ずどれかの作業が実施されていることに注意する。このことから、「後始末」作業の最早開始時刻より前にプロジェクトを完了させることは不可能である。

したがって、上のアルゴリズムによって計算された「後始末」作業の最早開始時刻がプロジェクトの最短所要時間に等しいことが分かる（プロジェクトの開始時刻を０としたので、「後始末」作業の最早開始「時刻」はプロジェクトの全作業を終了するまでの所要時間になる）。

このような作業列をクリティカルパスと言う。パス上のどの一つの作業の開始時刻が遅れてもプロジェクトが最短で完了しない、という意味で「クリティカル（重大な）」と名付けられている。クリティカルパスを構成する作業は、次の計算で機械的に求めることができる。

最遅終了時刻

ある作業の最遅終了時刻(latest finish time, LS)とは、「後始末」作業の最早開始時刻を遅らせないという条件の下で、その作業が終了していなければいけないぎりぎりの時刻のこと。ある作業の最遅終了時刻からその作業の作業時間を引いたものを最遅開始時刻(latest start time, LF)と言う。最早時刻とは、できる作業はなるべく早く済ませようとした計画した場合の時刻で、最遅時刻とは、決められた範囲で作業着手をなるべく遅らせようとした場合の時刻、ということができる。

各作業の最遅終了時刻、最遅開始時刻は次のようにして計算できる。

「後始末」作業の最早開始時刻を、その作業の最遅開始時刻とする。
最遅開始時刻が計算された作業だけを直接の後続作業とする作業の最遅終了時刻を、すべての後続作業の最遅開始時刻の最小値とし、それから作業時間を引いたものを最遅開始時刻とする。

このアルゴリズムにより、すべての作業の最遅終了時刻と最遅開始時刻が計算される。最遅開始時刻と最早開始時刻の差は、いわばゆとりの時間といってもよい。クリティカルパス上の作業は休み無く実施しなければいけないので、そのゆとり時間が無い作業が連なっている。そこで、各作業のゆとり時間を計算することにより、クリティカルパスを構成する作業を特定出来ることが期待される。

余裕時間とクリティカルパス

ある作業の全余裕時間(total float time, TF)とは、他の作業はすべて着手できる時刻に必ず着手すること、プロジェクトは最短所要時間で終わること、という条件の下で、その作業の開始を遅らせることが出来る時間の上限のことを言う。これに対して、ある作業の自由余裕時間(free float time, FF)とは、その作業のすべての後続作業が最早開始時刻に開始できるという条件の下で、その作業の開始を遅らせることが出来る時間の上限のことを言う。自由余裕時間は、すべての先行作業が予定通り進行しているという条件の下で、後続作業に迷惑を掛けずに（自由に）開始時刻を遅らせることが出来るゆとり時間という事ができる。これに対して、全余裕時間は、すべての先行作業が予定通り進行していて、すべての後続作業はいつでも着手できるという条件の下で、開始時刻を遅らせること出来るゆとり時間である。

ある作業の全余裕時間はその作業の最遅終了時刻（それまでに終えればプロジェクトは最短所要時間で完了する）から最早終了時刻（先行作業を含め、作業が予定通り終了している）を引いたもので与えられる。自由余裕時間は、後続作業の最早開始時刻までに作業を終えていれば良いと考え、すべての後続作業の最早開始時刻の最小値から、その作業の最早終了時刻を引いたものとして与えられる。

すべての作業の作業見積もり時間と先行後続関係が与えられると、それらから最早時刻、最遅時刻が計算され、それをもとに余裕時間が計算出来るので、全余裕時間のない作業を特定することができる。それらを順番に並べたものがクリティカルパスである。クリティカルパスは1本とは限らないが、この計算で、すべてを同時に求めることが出来る。

ＲによるPERT計算プログラム

「部分作業の名称」、「各部分作業の作業見積もり時間」、「各作業の先行作業群」を与えて、「プロジェクトの最短所要時間」と各作業の「最早開始時刻」「最遅完了時刻」「全余裕時間」「自由余裕時間」を計算するRのプログラムを以下に示す。

データの準備

データはExcelで生成し、それをコピーすることを前提に作られている。作業記号は適当な文字列（アルファベットなど）、先行作業群は「,」区切りとします。先行作業のない作業の先行作業欄は空白ではなく、「-」を入力する。

以下、同様
	A	B	C
1	作業記号	作業時間	先行作業
2	A	3	-
3	B	4	-
4	C	5	A,B

データの読み込み（作業記号、作業時間、先行作業列）

Excelで、上のようなデータを作り、ヘッダも含めてn+1行3列（n は作業の個数）のデータをコピーしたあと、Ｒを立ち上げ、 read.table 関数でデータを取り込む（mac の場合は read.delim 関数）。

> (original = read.table("clipboard", header=TRUE, stringsAsFactors=FALSE))
> # (original = read.delim(pipe("pbpaste"), header=TRUE, stringsAsFactors=FALSE))
   作業 作業時間 先行作業
1     A        3        -
2     B        4        -
3     C        5        -
4     D        5        A
5     E        2        A
6     F        3        B
7     G        6      B,C
8     H        6      E,F
9     I        2        D
10    J        3      H,I
11    K        4    G,H,I

表形式のデータをコピーペーストで取り込むために、windows では read.table("clipboard")>、mac では read.delim(pipe("pbpaste")) を実行する。header=TRUE はデータの１行目に項目名が書かれていることを指示するオプション、stringAsFactors=FALSE は文字型データを文字型データとして取り込むことを指示するオプションである（これがないと、あとの操作が面倒になる）。

取り込んだ表の右にクリティカルパスを計算するために必要なデータを保存する列を追加する。数値と文字が混在するので、data.frame 関数を使って、２次元の表をデータフレーム型として扱う。後々の計算式を読みやすいものにするために、行、列に名前をつけておく。colnames 関数は列に、rownames 関数は行に名前を付ける。

> pert = data.frame(originalData, matrix(-1,nrow=nrow(originalData),ncol=8))
> pert[,4] = "-"
> colnames(pert) = c("ID", "time", "prec", "succ", "ES", "EF", "LS", "LF", "TF", "FF", "CP")
> rownames(pert) = pert[,"ID"]
> pert
  ID time  prec succ ES EF LS LF TF FF CP
A  A    3     -    - -1 -1 -1 -1 -1 -1 -1
B  B    4     -    - -1 -1 -1 -1 -1 -1 -1
C  C    5     -    - -1 -1 -1 -1 -1 -1 -1
D  D    5     A    - -1 -1 -1 -1 -1 -1 -1
E  E    2     A    - -1 -1 -1 -1 -1 -1 -1
F  F    3     B    - -1 -1 -1 -1 -1 -1 -1
G  G    6   B,C    - -1 -1 -1 -1 -1 -1 -1
H  H    6   E,F    - -1 -1 -1 -1 -1 -1 -1
I  I    2     D    - -1 -1 -1 -1 -1 -1 -1
J  J    3   H,I    - -1 -1 -1 -1 -1 -1 -1
K  K    4 G,H,I    - -1 -1 -1 -1 -1 -1 -1

後続作業列の作成

ある作業の後続作業とは、その作業を先行作業として認識しているすべての作業のことである。作業Bの先行作業リストに作業Aがあれば、作業Bは作業Aにとって後続作業になるので、作業A の後続作業欄に作業名Bを追加する。for 文の制御変数にある「a in pert[,"ID"]」は「全ての作業に対して」という意味を持つ。先行作業リストはカンマ区切りなので、strsplit 関数を使って分解し、それらを文字型データとして扱うために unlist 関数を使用している。paste 関数をsep="" オプションをつけて実行すると、文字列を空白を挟まないでつなげた文字列を生成する。後続作業がある場合、最初の２文字が「=,」となっているので、それを消去しておく必要がある。それが２つ目のfor文である。substr 関数は文字列の部分列を取り出し、nchar 関数は文字列の長さを返す。

> for(a in pert[,"ID"]) {
+   if(pert[a,"prec"] == "-") next
+   d = unlist(strsplit(pert[a,"prec"],","))
+   for(b in d) 
+     pert[b,"succ"] = paste(pert[b,"succ"], ",", a, sep="")
+ }
> for(a in pert[,"ID"]) {	
+   if(regexpr(",", pert[a,"succ"]) > 0) 
+     pert[a,"succ"] = substr(pert[a,"succ"], 3, nchar(pert[a,"succ"]))	
+ }
> pert
  ID time  prec succ ES EF LS LF TF FF CP
A  A    3     -  D,E -1 -1 -1 -1 -1 -1 -1
B  B    4     -  F,G -1 -1 -1 -1 -1 -1 -1
C  C    5     -    G -1 -1 -1 -1 -1 -1 -1
D  D    5     A    I -1 -1 -1 -1 -1 -1 -1
E  E    2     A    H -1 -1 -1 -1 -1 -1 -1
F  F    3     B    H -1 -1 -1 -1 -1 -1 -1
G  G    6   B,C    K -1 -1 -1 -1 -1 -1 -1
H  H    6   E,F  J,K -1 -1 -1 -1 -1 -1 -1
I  I    2     D  J,K -1 -1 -1 -1 -1 -1 -1
J  J    3   H,I    # -1 -1 -1 -1 -1 -1 -1
K  K    4 G,H,I    # -1 -1 -1 -1 -1 -1 -1

最早開始時刻(ES)、最早終了時刻(EF)の計算

先行作業のない作業の最早開始時刻は0とし、最早終了時刻はその作業の作業時間とする。

> a = which(pert[,"prec"]=="-")
> pert[a,"ES"] = 0
> pert[a,"EF"] = pert[a,"time"]

先行作業のある作業の最早開始時刻は、全ての先行作業が終了する最も遅い時刻である。したがって、全ての先行作業の最早終了時刻が計算されていないと確定しない。そのために、最早終了時刻が計算された作業の集合を把握しておく必要がある。次のプログラム例の a がそれにあたる。setdiff(A, B) は集合 A から集合 B の要素を除いた部分集合を返す関数である。is.element(A,B) は集合 A の各要素が集合 B に含まれていれば TRUE、さもなければ FALSE とする論理値ベクトルを返す関数である。all 関数は引数の論理値ベクトルの全ての要素が TRUE のときだけ TRUE を返す。

> while(length(which(pert[,"ES"] < 0)) > 0) {
+ 	(a = pert[which(pert[,"ES"] >= 0),"ID"])				# 計算済み作業集合
+ 	for(b in setdiff(pert[,"ID"], a)) {				# a 以外の作業集合について計算
+ 		c = unlist(strsplit(pert[b,"prec"],","))
+ 		if(all(is.element(c,a))) {				# 先行作業は全て計算済み？
+ 			pert[b,"ES"] = max(pert[c,"EF"])
+ 			pert[b,"EF"] = pert[b,"ES"] + pert[b,"time"]
+ 		}
+ 	}
+ }
> pert
  ID time  prec succ ES EF LS LF TF FF CP
A  A    3     -  D,E  0  3 -1 -1 -1 -1 -1
B  B    4     -  F,G  0  4 -1 -1 -1 -1 -1
C  C    5     -    G  0  5 -1 -1 -1 -1 -1
D  D    5     A    I  3  8 -1 -1 -1 -1 -1
E  E    2     A    H  3  5 -1 -1 -1 -1 -1
F  F    3     B    H  4  7 -1 -1 -1 -1 -1
G  G    6   B,C    K  5 11 -1 -1 -1 -1 -1
H  H    6   E,F  J,K  7 13 -1 -1 -1 -1 -1
I  I    2     D  J,K  8 10 -1 -1 -1 -1 -1
J  J    3   H,I    # 13 16 -1 -1 -1 -1 -1
K  K    4 G,H,I    # 13 17 -1 -1 -1 -1 -1

最遅開始時刻(LS)、最遅終了時刻(LF)の計算

すべての作業の最早終了時刻の最大値がプロジェクトの最短完了時刻になる。後続作業のない作業の最遅終了時刻はプロジェクトの最短完了時刻とし、最遅開始時刻はその作業の作業時間を引いたものとする。

> proctime = max(pert[,"EF"])
> a = which(pert[,"succ"]=="-")
> pert[a,"LF"] = proctime
> pert[a,"LS"] = proctime - pert[a,"time"]

後続作業がある場合は、後続作業の最遅開始時刻までに終了していなければいけないという制約から、全ての後続作業の最遅開始時刻の中の最小値とする。したがって、全ての後続作業の最遅開始時刻が計算されていないと確定しない。そのために、最遅開始時刻が計算された作業の集合を把握しておく必要がある。計算手順は、先の最早開始時刻、最早終了時刻の計算とほとんど同じ。

> while(length(which(pert[,"LF"] < 0)) > 0) {
+ 	(a = pert[which(pert[,"LF"] >= 0),"ID"])				# 計算済み作業集合
+ 	for(b in setdiff(pert[,"ID"], a)) {				# a 以外の作業集合について計算
+ 		c = unlist(strsplit(pert[b,"succ"],","))		
+ 		if(all(is.element(c,a))) {				# 先行作業は全て計算済み？
+ 			pert[b,"LF"] = min(pert[c,"LS"])
+ 			pert[b,"LS"] = pert[b,"LF"] - pert[b,"time"]
+ 		}
+ 	}
+ }
> pert
  ID time  prec succ ES EF LS LF TF FF CP
A  A    3     -  D,E  0  3  2  5 -1 -1 -1
B  B    4     -  F,G  0  4  0  4 -1 -1 -1
C  C    5     -    G  0  5  2  7 -1 -1 -1
D  D    5     A    I  3  8  6 11 -1 -1 -1
E  E    2     A    H  3  5  5  7 -1 -1 -1
F  F    3     B    H  4  7  4  7 -1 -1 -1
G  G    6   B,C    K  5 11  7 13 -1 -1 -1
H  H    6   E,F  J,K  7 13  7 13 -1 -1 -1
I  I    2     D  J,K  8 10 11 13 -1 -1 -1
J  J    3   H,I    - 13 16 14 17 -1 -1 -1
K  K    4 G,H,I    - 13 17 13 17 -1 -1 -1

全余裕時間(TF)、自由余裕時間(FF)の計算

ある作業の全余裕時間は、その作業の最遅終了時刻から最早終了時刻を引いたもので与えられる。

自由余裕時間は全ての後続作業が最早開始時刻に開始できるという条件があるので、そういう条件を必要としない後続作業のない作業の自由余裕時間は全余裕時間と等しい。

後続作業がある場合は、すべての後続作業の最早開始時刻の最小値から、最早終了時刻を引いたものが自由余裕時間になる。

> pert[,"TF"] = pert[,"LF"] - pert[,"EF"]
> for(a in pert[,"ID"]) {
+ 	if(pert[a,"succ"]=="-") {
+ 		pert[a,"FF"] = pert[a,"TF"]
+ 	} else {
+ 		b = unlist(strsplit(pert[a,"succ"], ","))
+ 		pert[a,"FF"] = min(pert[b,"ES"]) - pert[a,"EF"]
+ 	}
+ }

クリティカルパス

余裕時間のない作業は予定通り開始終了しないとプロジェクトの最短時間を達成できないという意味でクリティカルと呼ばれ、それらの作業をつなげたものをクリティカルパスと呼ぶ。クリティカルパスを構成する余裕のない作業に印をつけて、PERT計算を終了する。

> pert[which(pert[,"TF"]== 0),11] = "*"
> pert
  ID time  prec succ ES EF LS LF TF FF CP
A  A    3     -  D,E  0  3  2  5  2  0 -1
B  B    4     -  F,G  0  4  0  4  0  0  *
C  C    5     -    G  0  5  2  7  2  0 -1
D  D    5     A    I  3  8  6 11  3  0 -1
E  E    2     A    H  3  5  5  7  2  2 -1
F  F    3     B    H  4  7  4  7  0  0  *
G  G    6   B,C    K  5 11  7 13  2  2 -1
H  H    6   E,F  J,K  7 13  7 13  0  0  *
I  I    2     D  J,K  8 10 11 13  3  3 -1
J  J    3   H,I    - 13 16 14 17  1  1 -1
K  K    4 G,H,I    - 13 17 13 17  0  0  *

> pert[which(pert[,"TF"]== 0),"ID"]
[1] "B" "F" "H" "K"

全余裕時間（TF）が0の作業がクリティカルパスを構成するので、この場合は「B→F→H→K」がクリティカルパスになります。

> z[which(z[,"TF"] == 0),1]
[1] "B" "F" "H" "K"

パッケージ化

データ行列を与えると、プロジェクトの最短所要時間とクリティカルパスを計算して返す関数 PERT は、以上のコードを関数定義の中に含めるだけです。以下に構成だけを示します。

この関数の戻り値は、プロジェクトの最短所要時間（）と、クリティカルパス上にある作業集合（と計算に使われた表）である。

# 入力データフレームは、「作業記号」「作業時間」「先行作業列」の3列分で、
# 　作業記号は英数字の文字列、先行作業列はカンマ区切りで作業記号を並べたものとする。
# 出力は、
# 　「最早開始時刻」「最早終了時刻」「最遅開始時刻」「最遅終了時刻」「全余裕時間」「自由余裕時間」
# 　　　　　　　　　　　　　　　　　　　（入力データフレームの5行目から10行目まで）
# 　「プロジェクト最短所要時間（projectTime）」
# 　「クリティカルパスの作業列（criticalPath）」

PERT = function(originalData) {
	pert = data.frame(originalData, matrix(-1,nrow=nrow(originalData),ncol=8))
	pert[,4] = "-"
	colnames(pert) = c("ID", "time", "prec", "succ", "ES", "EF", "LS", "LF", "TF", "FF", "CP")
	rownames(pert) = pert[,"ID"]
	# 後続作業リスト作成
	for(a in pert[,"ID"]) {
		if(pert[a,"prec"] == "-") next
		d = unlist(strsplit(pert[a,"prec"],","))
		for(b in d) 
			pert[b,"succ"] = paste(pert[b,"succ"], ",", a, sep="")
	}
	for(a in pert[,"ID"]) {
  	if(regexpr(",", pert[a,"succ"]) > 0) 
    		pert[a,"succ"] = substr(pert[a,"succ"], 3, nchar(pert[a,"succ"]))
	}
 
	# 最早開始、最早完了時刻
	# 先行作業なし
	a = which(pert[,"prec"]=="-")
	pert[a,"ES"] = 0
	pert[a,"EF"] = pert[a,"time"]
	# 先行作業あり
	while(length(which(pert[,"ES"] < 0)) > 0) {
  		a = pert[which(pert[,"ES"] >= 0),"ID"]			# 計算済み作業集合
  		for(b in setdiff(pert[,"ID"], a)) {			# a 以外の作業集合について計算
    			c = unlist(strsplit(pert[b,"prec"],","))
    			if(all(is.element(c,a))) {			# 先行作業は全て計算済み？
      				pert[b,"ES"] = max(pert[c,"EF"])
      				pert[b,"EF"] = pert[b,"ES"] + pert[b,"time"]
    			}
  		}
	}

	# 最遅開始、最遅完了時刻
	proctime = max(pert[,"EF"])
	# 後続作業なし
	m = which(pert[,"succ"]=="-")
	pert[m,"LF"] = proctime
	pert[m,"LS"] = proctime - pert[m,"time"]

	# 後続作業あり
	while(length(which(pert[,"LF"] < 0)) > 0) {
  		a = pert[which(pert[,"LF"] >= 0),"ID"]			# 計算済み作業集合
  		for(b in setdiff(pert[,"ID"], a)) {			# a 以外の作業集合について計算
    			c = unlist(strsplit(pert[b,"succ"],","))
    			if(all(is.element(c,a))) {			# 先行作業は全て計算済み？
      				pert[b,"LF"] = min(pert[c,"LS"])
      				pert[b,"LS"] = pert[b,"LF"] - pert[b,"time"]
    			}
  		}
	}

	# 余裕時間
	pert[,"TF"] = pert[,"LF"] - pert[,"EF"]
	for(a in pert[,"ID"]) {
	  	if(pert[a,"succ"]=="-") {
    			pert[a,"FF"] = pert[a,"TF"]
  		} else {
    			b = unlist(strsplit(pert[a,"succ"], ","))
    			pert[a,"FF"] = min(pert[b,"ES"]) - pert[a,"EF"]
  		}
	}
	# クリティカルパス
	pert[which(pert[,"TF"]== 0),11] = "*" 
	CP = pert[which(pert[,"CP"]=="*"),"ID"]

	return(list(ProjectTime=proctime, criticalPath=CP, table=pert))
}

計算例は次の通り（最早開始時刻を上から順番に計算できない例）。

> z = read.table("clipboard", header=TRUE, stringsAsFactors=FALSE)
> PERT(z)
$table
  ID time  prec succ ES EF LS LF TF FF
A  A    3     - D,E  0  3  2  5  2  0
B  B    4     - F,G  0  4  0  4  0  0
C  C    5     -   G  0  5  2  7  2  0
D  D    5     A   I  3  8  6 11  3  0
H  H    6   E,F K,J  7 13  7 13  0  0
E  E    2     A   H  3  5  5  7  2  2
F  F    3     B   H  4  7  4  7  0  0
G  G    6   B,C   K  5 11  7 13  2  2
K  K    4 G,H,I   - 13 17 13 17  0  0
I  I    2     D K,J  8 10 11 13  3  3
J  J    3   H,I   - 13 16 14 17  1  1

$projectTime
[1] 17

$criticalPath
[1] "B" "H" "F" "K"

もどる

ＰＥＲＴ計算、作業時間が確率変動する場合

PERT計算の弱点の一つは、作業時間が固定されていることです。作業時間が事前に分かっていることはまれで、特に未知の作業に対しての見積もり時間が確実に予測できるということは難しいでしょう。作業見積もり時間がばらつく場合の最短所要時間は確率計算が必要になりますが、ここでは、作業見積もり時間の標本に対してPERT計算を実行し、最短所要時間を計算する、ということを多数回繰り返してその統計的性質を調べる、というモンテカルロ法を使います。

simPERT = function(z, vm=3) {
	z[,"time"] = round((rbeta(nrow(z),vm,vm)+0.5) * z[,"time"] * 1000, 0)
	prt = PERT(z)
	tb = prt$table
	tb = data.frame(tb[,1], tb[,2]/1000, tb[,3:4], tb[,5:10]/1000)
	return(list(ptime=prt$projectTime/1000, cp=prt$criticalPath, tb=tb))
}

注釈

simPERT() 関数は、データ行列 z（作業記号、平均作業時間、先行作業列）と作業時間のばらつきのパラメータ vm を与えて、作業時間の標本を生成し、PERT計算を実行し、プロジェクト最短所要時間とそのときのクリティカルパス上の作業列を返す。
作業時間は、平均作業時間の0.5倍から1.5倍までの間で左右対称のベータ分布に従うとしている。rbeta(n,a,b) 関数は、パラメータ a,b のベータ乱数を n 個生成する。ここでは a=b としているので、左右対称となり、正規分布を有限で打ち切ったような形をしているとした。この場合の標準偏差は 0.5/√(2*vm+1) である。
計算誤差をなくすために、作業時間の標本値は小数点4桁未満を四捨五入し、それを1000倍することによって整数化し、PERT計算を整数で実行している。

実行例

作業時間について1000組の標本を生成し、1000通りのネットワークについてクリティカルパスと最短所要時間を計算して、それらの統計量を計算したのが次のプログラムです。最短所要時間については、平均と標準偏差、それにヒストグラム、クリティカルパスについては、作業の組合せを標本値として度数分布を作り棒グラフ化してあります。クリティカルパスについては相対頻度が1%以上のものだけを表示させてあります。

z = read.table("clipboard", header=TRUE, stringsAsFactors=FALSE)
names(z) = c("ID", "time", "prec")
ptime = numeric(0)
cpath = character(0)
for(i in 1:1000) {
	prj = simPERT(z,3)
	ptime = c(ptime, prj$ptime)
	cpath = c(cpath, paste(prj$cp, collapse=""))
}
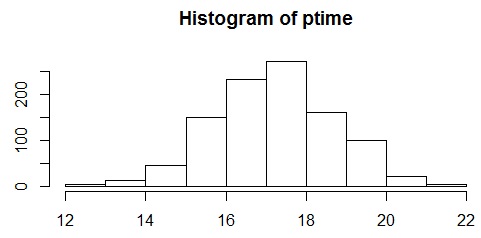
hist(ptime)
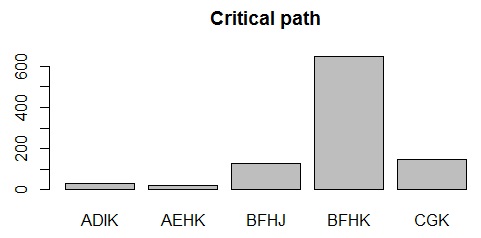
barplot(table(cpath)[which(table(cpath)<10)], main="Critical path")

注釈

最短所要時間を集めたもの ptime はヒストグラムにまとめる。hist() は、与えられた数値データのヒストグラムを描く関数である。
クリティカルパス上の作業は集合として意味があるので、作業記号をつなげたものを文字列に変換して、その度数分布を計算し、棒グラフを描いている。barplot() は、与えられた度数分布の棒グラフを描く関数である。table() は、度数分布を計算する関数である。ここでは、度数が10より大きいものだけを取り出して棒グラフを描いている。main オプションはグラフのタイトルを書く。

計算例

確率変動しない場合のPERT計算で例に出した作業例（ここ）の場合、1000回のシミュレーションで、最短所要時間の平均は 17.22、標準偏差は 1.47 でした。確率変動を考慮しない場合の最短所要時間は17でしたので、やや長めという結果になりました。ばらつきを考えると、通常の（非確率的な）PERT計算による最短所要時間の2割増しくらいの遅れを考えた方が良いということが分かります。

クリティカルパスは、約65%が確率変動しない場合のクリティカルパス「B→F→H→K」と一致しましたが、確率変動により平均値が15の「C→G→K」が 15%、同じく平均値が15の「B→E→H→J」が13% 計測されました。

当然のことながら、この遅れは各作業のばらつき具合に大きく依存します。ベータ分布のパラメータを調整して、標準偏差を約4割小さくした場合、約9割は確率変動しない場合のクリティカルパスに一致し、最短所要時間の平均は17.06、標準偏差は0.96という数値が得られています。

> c(mean(ptime), sd(ptime))
[1] 17.223562  1.472551
> table(cpath)
cpath
  ADIJ   ADIK   AEHJ   AEHK BCFGHK   BFHJ  BFHJK   BFHK    BGK    CGK 
     5     32      7     22      1    129      1    647      8    148

　　　　　最短所要時間

　　　　　クリティカルパス

もどる