目次
システム分析の一つの方法で、将来に起こりうるかもしれない出来事を、コンピュータを使って仮想的に実現するということを繰り返し、その結果を参考にしてシステムの仕組みを解き明かそうとするものです。
一般に、一様乱数とは、一様分布に従う乱数のことですが、何も特別に注意しない場合は、一様分布として区間 [0,1] の連続一様分布を仮定することが普通です。区間の端点は含めたり含めなかったりします。
Rには一様乱数を生成する関数として runif() が用意されています。例えば、runif(10) とすると、10 個の一様乱数が生成されます。runif(100, a, b) とすると、区間 [a,b] で一様分布する一様乱数が 100 個生成されます。
コンピュータは扱う数が離散なので、実際に生成される乱数は最小数を単位とする離散一様分布に従う乱数になりますが、実用上は問題になることはないでしょう。
sample() は離散一様乱数を生成する関数です。例えば、sample(6, 1) とすると、サイコロを一回振ったときに出る目のような(1から6までの中からランダムに選ばれた)数が生成されます。sample(6, 10, replace=T) とすると、サイコロを10回振ったときに出る目のような数列が生成されます。
> runif(10)
[1] 0.44345384 0.55170438 0.07933719 0.84818667 0.13661365 0.04789409
[7] 0.79414594 0.45976199 0.78238876 0.83182575
> table(cut(runif(100000), seq(0,1,0.1)))
(0,0.1] (0.1,0.2] (0.2,0.3] (0.3,0.4] (0.4,0.5] (0.5,0.6] (0.6,0.7]
9927 10099 9968 10006 9915 10048 10024
(0.7,0.8] (0.8,0.9] (0.9,1]
9847 10118 10048
> sample(6,1)
[1] 4
> sample(6,10,replace=T)
[1] 6 6 6 2 5 5 6 1 2 1
> table(sample(6,60000,replace=T))
1 2 3 4 5 6
9945 9868 10254 10042 10008 9883
ただし、table() は度数分布を生成する関数、cut() は数を小区間に分けて名前付けする関数です。一様分布と言っても、実際に生成される数列にはこの程度のばらつきがあるということを認識しておいてください。
注意しなければいけないのは、「乱数」と言っても(数学関数と同じように)あらかじめプログラム化された関数によって生成(計算)されているということです。Rを立ち上げて最初に runif(10) を実行すると、常に上のような数列が表示されます(v.3.0.2 の場合)。初期状態が同じならば、生成される関数値は同じになるのは当然です。続いて実行される table(), sample() などの実行結果も全く同じになりますが、これでは「真の」乱数にはなりません。その意味で、コンピュータによって生成される乱数「もどき」の数を擬似乱数と言いますが、了解されている場合は、単に乱数と言います。
初期状態を変えるために set.seed() という関数が用意されています。 任意の整数を引数として指定して関数を実行すると、初期状態が違う乱数が生成されます。通常は、同じ乱数列を使いたくないとき、プログラムの先頭で一回だけこの関数を実行させます。同じ引数を使って set.seed() を実行すると、予想されるように、同じ乱数列が生成されます。
> set.seed(1) > runif(5) [1] 0.2655087 0.3721239 0.5728534 0.9082078 0.2016819 > set.seed(11111) > runif(5) [1] 0.5014483 0.9702328 0.7876004 0.9022259 0.8141778 > set.seed(1) > runif(5) [1] 0.2655087 0.3721239 0.5728534 0.9082078 0.2016819
常に同じ数が生成されることには意味があります。
Matsumoto(1998)によるパラメータを使用
p = 25 # GF(2)係数原始3項式
q = 11 #
m = 16 # 語長
(a = c(1,0,1,0, 1,0,0,0, 0,1,1,1, 0,1,0,1)) # 定数ベクトル
(tg = matrix(sample(0:1, (p+1)*m, replace=T), p+1)) # 初期値
n = 20000
for(i in 1:n) {
y = c(0, tg[i,-m])
if(tg[i,m] == 1) (y = xor(y,a)) # 末尾のビットが奇数の場合
tg = rbind(tg,y) # テストのため、全部記憶させる
}
y = tg[,1]
for(i in 2:m) y = 2*y + tg[,i] # 十進数に変換
plot(table(cut(y,128)), type="h") # 一様性のチェック
一様分布以外の確率分布に従う乱数は、一様乱数を変換して作り出します。例えば、二つの一様乱数の最小値は、0以上1以下で0となる可能性が最大の三角形状の密度関数に従う乱数になります。二つの一様乱数の和は、0以上2以下で、1が最大となる三角形状の密度関数に従う乱数になります。
> rtriag = function(n=2) min(runif(n))
> table(cut(sapply(rep(2,10000), rtriag),seq(0,1,0.1))) (0,0.1] (0.1,0.2] (0.2,0.3] (0.3,0.4] (0.4,0.5] (0.5,0.6] (0.6,0.7] 1871 1704 1531 1301 1111 912 676 (0.7,0.8] (0.8,0.9] (0.9,1] 492 305 97
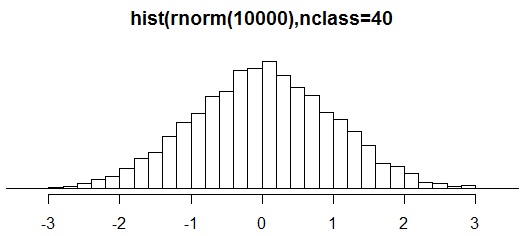
Rは統計計算のパッケージとして作られているので、名前の付いた確率分布に従う乱数については、それを生成する専用の関数が用意されています。確率分布を表す固有名詞の前に「r」を付けたものがそれです。例えば、rnorm() は正規乱数を、rexp() は指数乱数を生成する関数です。
| 正規分布 | rnorm(n, m, s) |
mは平均、sは標準偏差 |
| 指数分布 | rexp(n, a) |
aは平均の逆数 |
| ガンマ分布 | rgamma(n, a, b) |
aは形状、bは尺度パラメータ |
| ベータ分布 | rbeta(n, a, b) |
a,bはベータ分布のパラメータ |
| 2項分布 | rbinom(n, N, p) |
N,pは2項分布のパラメータ |
| ポアソン分布 | rpois(n, d) |
dは平均値 |
nは生成する乱数の個数です。標準正規乱数の場合はm,sを省略することが出来ます。次は正規乱数10000個を生成して、そのヒストグラムを描いたものです。
離散分布の場合は、sample() 関数を使い、離散確率分布指定のオプション「prob=...」を利用して生成します。sample() 関数の最初の引数は取り得る数の集合、2番目は生成する個数、3番目は復元抽出するために「replace=T」、4番目に分布指定のためのベクトル「prob=...」を書きます。分布指定のベクトルは、確率そのものでなくても、相対的な大きさが分かるものであれば構いません。例えば、次は1と6の目が他の目に比べて2倍出やすいというサイコロを振ったときに出る目を生成するものです。
> sample(1:6,20,prob=c(2,1,1,1,1,2),replace=T)
[1] 6 2 6 1 1 4 5 6 4 1 1 6 3 6 3 2 4 6 1 5 > table(sample(1:6,8000,replace=T,prob=c(2,1,1,1,1,2)))
1 2 3 4 5 6 2013 992 971 1000 1038 1986
rnorm(10) ## 標準正規乱数 runif(10) ## 「標準」一様乱数 rbinom(10, 5, 0.5) ## 2項乱数(n=5,p=0.5) rexp(10, 2) ## 率2の指数乱数 ## 一様乱数の初期値設定 set.seed(11212221) ## 離散分布からのサンプリング sample(c(0,1), size=10, replace=T, prob=c(1,10)) ## 歪んださいころ投げ hist(sample(6,100,prob=c(2,1,1,1,1,2),replace=T)+0.01) ## ランダム置換 sample(0:9)
ある図形の面積を計算する方法として、次のようなものがあります。その図形を含む正方形、あるいは長方形のような、面積が簡単に計算出来る規則図形を描き、その規則図形に小さな芥子粒を敷き詰めます。目的の図形の上にある芥子粒の数を全体の芥子粒の個数で割ったものに規則図形の面積を掛ければ、目的の図形の面積にほぼ等しい数値を得ることが期待できます。芥子粒を数える代わりに、規則図形の中にランダムな点を無数にばらまき、目的の図形の上に落ちる点の相対個数を計算しても同じです。これならば乱数を使ってコンピュータで実験できます。
4分円を正方形で囲み、2つの一様乱数のペア (x,y) をその正方形に落としたランダムな点と考えると、4分円に含まれるのは x2+y2 < 1 が成り立つ場合と考えること出来ます。このような実験を無数に繰り返して、4分円に含まれた実験の相対回数を計算すると、それが4分円の面積、すなわち円周率を4で割ったものに近いものが得られるはずです。
> mean(runif(10000)^2+runif(10000)^2 < 1) * 4 [1] 3.1036
> n = 1000; m = 10000 > z = sapply(1:n, function(x) mean(runif(m)^2+runif(m)^2 < 1) * 4) > c(mean(z), mean(z)-2*sd(z)/sqrt(n), mean(z)+2*sd(z)/sqrt(n)) [1] 3.141473 3.140417 3.142530
最後の4行は、m=10000回の実験を繰り返して一つの推定値を得るという実験をn=1000回繰り返し、その結果から得られる推定値と、その95%信頼区間を計算するという実験のプログラムとその結果です。
Arctan() の公式を使うと、1/(1+x2) を区間 [0,1] で定積分したものは円周率の4分の1に等しくなります。定積分する代わりに、被積分の関数値をたくさん計算してそれらを平均すれば、定積分の推定値が計算出来ることを利用すると、円周率の数値を「推定」することが出来ます。
> mean(4/(1+runif(10000)^2)) [1] 3.139376
> n = 1000; m = 10000 > z = sapply(1:n, function(x) mean(4/(1+runif(m)^2))) > c(mean(z), mean(z)-2*sd(z)/sqrt(n), mean(z)+2*sd(z)/sqrt(n)) [1] 3.141518 3.141109 3.141927
誤差の減り方を見るための関数
mctest <- function (N){
e = rep(0, N/10)
r = runif(N)
z = 0
for (i in 1:N) {
z = z + 4/(1+r[i]*r[i])
if (i%%10 == 0) e[i/10] = log(abs(z/i - pi))
}
plot(e) ### 誤差の推移
return(z/N)
}
mctest(10000)
n = 10000;
x = runif(n, -1, 1); y = runif(n, -1, 1);
ix = which(x^2+y^2 < 1);
plot(x[-ix], y[-ix], xlim=c(-1,1), ylim=c(-1,1));
par(new=T)
plot(x[ix], y[ix], col=2, xlim=c(-1,1), ylim=c(-1,1));
n = 100000; L = 1; b = 0.7 * L
x = runif(n, 0, 1); y = runif(n, 0, 1);
2*b/L/mean(x < b / L * cos(y * pi/2))
m = 4; n = 100000;
z = sapply(1:n, function(x) sum(sample(1:m) * (1:m)))
hist(z, freq=F)
(1-1/n)n -> e-1 となることと、n 個の玉を n 個の箱の中にランダムに入れる時、任意に選んだ一つの箱に玉が一つも入らない確率は (1-1/n)n であることを組み合わせると、ネピアの数 e をモンテカルロ実験で「推定」出来る。
nepia = function(N = 10000) {
r = sample(N, N, replace=T) # 復元抽出、玉と箱の番号を対応
return(N / (N - length(table(r)))) # 玉の個数の度数分布を計算し、玉のない箱の数を算出
}
N = 10000
M = 100
w = sapply(rep(N, M), nepia) # N を与えて、M 個の推定結果を得る
hist(w, main=paste("m =", round(mean(w), 4), "sd =", round(sd(w)/sqrt(M), 4)))
# 計算例
> c(mean(w), sd(w)/sqrt(M))
[1] 2.716767669 0.002138369
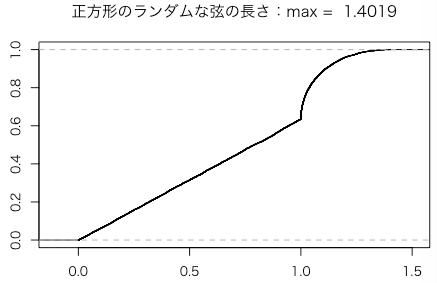
一つの辺を固定し、始点をその辺からランダムに選ぶ。始点から弦を引く方向をランダムに選び、正方形と交わる点を終点として「ランダムな」弦を決める。終点が始点のある辺と平行な対辺か、左の辺か右の辺かで計算方式が変わる。
radar = function(n = 1000) {
x = runif(n, 0, 1) # ランダムな始点
t = runif(n, 0, pi) # ランダムな方向
z = ifelse(t < pi/2 & (1-x)*tan(t) < 1, (1-x) / cos(t), # 弦の長さの計算
ifelse(t > pi/2 & -x*tan(t) < 1, -x / cos(t), 1 / sin(t))) # 左辺、右辺、対辺の順
return(z)
}
n = 1000
z = radar(n)
plot(ecdf(z))
次は一つの実行例である。

mu = -5; sg = 1;
nu = 5; ta = 3;
rho = -0.8
n = 1000;
r2norm = function(mu=-4,sg=1, nu=4, ta=2, rho=0.5, n=1000) {
x = sg * rnorm(n) + mu
y = ta * sqrt(1-rho^2) * rnorm(n) + ta/sg*rho*(x-mu) + nu
return(list(x=x,y=y));
}
z = r2norm(n=1000)
plot(z$x,z$y)
## 2変量正規乱数、その2
n = 2000; mx = 10; sx = 3; my = 20; sy = 5; r = -0.8
y = rnorm(n, my, sy)
x = rnorm(n, mx + r*sx/sy * (y - my), sx*sqrt(1-r^2))
plot(x,y)
## グラフィックス:等高線
library(gregmisc)
c(mean(x), sd(x), mean(y), sd(y), cor(x,y))
h2d = hist2d(x, y, show=F, nbins=c(20,20)) # 2次元の度数分布
filled.contour(h2d$x, h2d$y, h2d$counts, nlevels=20, col=gray((25:0)/25))
対称な長さ 2n のランダムォークで最後に原点を訪問する時点に関して、時点 1 以降は原点に戻らない(すなわち、時点 0 が最後の訪問)と、2n でちょうど原点に戻る確率が同じで最大になり、その間は左右対称で U 字型の確率関数になる。次は、その法則を実際の例で検証するためのモンテカルロ実験の例である。
lastVisit = function(n) {
b = sample(c(-1,1), n, replace=T) ## コイン投げ
b[1] = 0; b = cumsum(b) ## 累積和
rev(which(b == 0))[1]
}
run = sapply(rep(100,1000), lastVisit) ## n=100 として1000回繰り返す
plot(table(run), type="h")
## 2変量正規乱数の標本プロット
normal2Plot = function(n=1000, rho=0.5) {
x = rnorm(n)
y = rho*x + sqrt(1-rho^2)*rnorm(n)
plot(x,y)
cor(x,y)
}
## 2変量正規分布の密度関数
dnorm2 = function(x=1, y=1, m1=0, s1=1, m2=0, s2=1, rho=0.5) {
zx = (x - m1) / s1; zy = (y - m2) / s2
exp(-(zx^2+zy^2-2*rho*zx*zy)/2/(1-rho^2)) /
(2*pi * s1 * s2 * sqrt(1-rho^2))
}
################################## 放射線量の分布 ############################
n = 1000; rho = 0.7
x = rt(n,3)
y = rho*x + sqrt(1-rho^2)*rt(n,3)
plot(x,y, type="n", xaxt="n", yaxt="n", xlim=c(-3,3),ylim=c(-3,3))
## ポワソン分布で強度決定
z = numeric(n);
for(i in 1:n) {
z[i] = q = rpois(1,2*exp(-sqrt((x[i]^2+y[i]^2))))+1
}
## 中心をずらして描画(変数変換:x+c/(1+x^2))
a = 0.04
for(i in 1:n) {
xa = x[i]-1/(1+0.25*x[i]^2); ya = y[i]-1/(1+0.25*y[i]^2);
rect(-xa,ya,-xa+z[i]*a,ya+z[i]*a)
if(z[i] >= 3) rect(-xa,ya,-xa+z[i]*a,ya+z[i]*a, col="orange")
}
## 強度の大きいところに色づけ
for(i in 1:n) {
xa = x[i]-1/(1+0.25*x[i]^2); ya = y[i]-1/(1+0.25*y[i]^2);
if(x[i]^2+y[i]^2 > 2 & z[i] >= 2)
rect(-xa,ya,-xa+z[i]*a,ya+z[i]*a, col="orange")
if(x[i]^2+y[i]^2 > 2 & z[i] >= 3)
rect(-xa,ya,-xa+z[i]*a,ya+z[i]*a, col=2)
if(z[i] >= 6) rect(-xa,ya,-xa+z[i]*a,ya+z[i]*a, col=2)
}
## 同心円を描く
t = seq(0,2*pi,0.1)
lines(cos(t)+1,sin(t)-1, col=2)
lines(2*cos(t)+1,2*sin(t)-1, lty=2, col=2)
lines(3*cos(t)+1,3*sin(t)-1, lty=2, col="orange")
ある図形の面積を計算する方法として、次のようなものがあります。その図形を含む正方形、あるいは 長方形のような、面積が簡単に計算出来る規則図形を描き、その規則図形に小さな芥子粒を敷き詰めます。目的の図形の上にある芥子粒の数を全体の芥子粒の個 数で割ったものに規則図形の面積を掛ければ、目的の図形の面積にほぼ等しい数値を得ることが期待できます。芥子粒を数える代わりに、規則図形の中にランダ ムな点を無数にばらまき、目的の図形の上に落ちる点の相対個数を計算しても同じです。これならば乱数を使ってコンピュータで実験できます。
4分円を正方形で囲み、2つの一様乱数のペア (x,y) をその正方形に落としたランダムな点と考えると、4分円に含まれるのは x2+y2 < 1 が成り立つ場合と考えること出来ます。このような実験を無数に繰り返して、4分円に含まれた実験の相対回数を計算すると、それが4分円の面積、すなわち円周率を4で割ったものに近いものが得られるはずです。
> mean(runif(10000)^2+runif(10000)^2 < 1) * 4 [1] 3.1036
> n = 1000; m = 10000 > z = sapply(1:n, function(x) mean(runif(m)^2+runif(m)^2 < 1) * 4) > c(mean(z), mean(z)-2*sd(z)/sqrt(n), mean(z)+2*sd(z)/sqrt(n)) [1] 3.141473 3.140417 3.142530
最後の4行は、m=10000回の実験を繰り返して一つの推定値を得るという実験をn=1000回繰り返し、その結果から得られる推定値と、その95%信頼区間を計算するという実験のプログラムとその結果です。
Arctan() の公式を使うと、1/(1+x2) を区間 [0,1] で定積分したものは円周率の4分の1に等しくなります。定積分する代わりに、被積分の関数値をたくさん計算してそれらを平均すれば、定積分の推定値が計算出来ることを利用すると、円周率の数値を「推定」することが出来ます。
> mean(4/(1+runif(10000)^2)) [1] 3.139376
> n = 1000; m = 10000 > z = sapply(1:n, function(x) mean(4/(1+runif(m)^2))) > c(mean(z), mean(z)-2*sd(z)/sqrt(n), mean(z)+2*sd(z)/sqrt(n)) [1] 3.141518 3.141109 3.141927
誤差の減り方を見るための関数
mctest <- function (N){
e = rep(0, N/10)
r = runif(N)
z = 0
for (i in 1:N) {
z = z + 4/(1+r[i]*r[i])
if (i%%10 == 0) e[i/10] = log(abs(z/i - pi))
}
plot(e) ### 誤差の推移
return(z/N)
}
mctest(10000)
n = 10000;
x = runif(n, -1, 1); y = runif(n, -1, 1);
ix = which(x^2+y^2 < 1);
plot(x[-ix], y[-ix], xlim=c(-1,1), ylim=c(-1,1));
par(new=T)
plot(x[ix], y[ix], col=2, xlim=c(-1,1), ylim=c(-1,1));
n = 100000; L = 1; b = 0.7 * L
x = runif(n, 0, 1); y = runif(n, 0, 1);
2*b/L/mean(x < b / L * cos(y * pi/2))
m = 4; n = 100000;
z = sapply(1:n, function(x) sum(sample(1:m) * (1:m)))
hist(z, freq=F)
平行線を引いた面に,無数の針を落としたとき、平行線に交わった針の相対本数を数えることによって,円周率が推定できるという円周率の実験的推定手順はビュ フォンの針実験として知られる。
次は、その実験により円周率の推定値を計算するプログラムの一例である。
> n = 1000
> L = 0.9
> px = runif(n, 0, 10)
> py = runif(n, 0, 10)
> pt = runif(n, 0, 1000)
> pz = cbind(px + L*cos(pt), px - L*cos(pt), py + L*sin(pt), py - L*sin(pt))
> ck = floor((pz[,3]+1)/2) != floor((pz[,4]+1)/2)
> cat("pihat =", 2*L/mean(ck), "\n")
pihat = 3.174603
針の落ちる様子をグラフ化するプログラムと実行例を示す。
> n = 1000
> L = 0.9
> px = runif(n, 0, 10)
> py = runif(n, 0, 10)
> pt = runif(n, 0, 1000)
> pz = cbind(px + L*cos(pt), px - L*cos(pt), py + L*sin(pt), py - L*sin(pt))
> ck = floor((pz[,3]+1)/2) != floor((pz[,4]+1)/2)
> cat("pihat =", 2*L/mean(ck), "\n")
pihat = 3.174603
# 実験のグラフ表示
> plot(0, xlim=c(0,10), ylim=c(0,10), type="n", axes=F, ann=F)
> points(px,py)
> zz = sapply(1:n, function(k) lines(pz[k,1:2], pz[k,3:4], col=ck[k]+1))
> abline(h=2*(1:5)-1)
○が針の中心、赤い線は平行線と交わっている針、黒い針は交わらなかった針を表している。 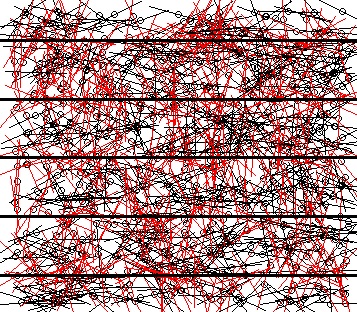
推定値の精度を知るには、乱数を変えて繰り返し、その結果のばらつきを統計処理すれば良い。最初に垂直線を1本引いて、落とした針を平行移動しその中心座標 がその垂直線上に来るようにしても推定結果は変わらないので、上に推定値を得る手順から px ベクトルを省略することが出来る。それを関数にまとめると,次 のようになる。
buffon <- function(n=1000, L=0.9) {
py <- runif(n, 0, 10)
pt <- runif(n, 0, 1000)
pz <- py + L*sin(pt)
pw <- py - L*sin(pt)
ck <- floor((pz+1)/2) != floor((pw+1)/2)
return(2*L/mean(ck))
}
これを sapply() 関数で繰り返し計算させれば良い。実験の回数(標本サイズ)を変えたときの 95%信頼区間を比較した結果の例を示す。
> n = 10000; m = 100
> zz = sapply(rep(n, m), buffon) > ci95 = 1.96 * sd(zz) / sqrt(m) > cat("円周率の信頼区間 ( n =", n, ") [", mean(zz)-ci95, mean(zz)+ci95, "]\n") 円周率の信頼区間 ( n = 10000 ) [ 3.13519 3.146718 ] > n = 1000; m = 100
> zz = sapply(rep(n, m), buffon) > ci95 = 1.96 * sd(zz) / sqrt(m) > cat("円周率の信頼区間 ( n =", n, ") [", mean(zz)-ci95, mean(zz)+ci95, "]\n") 円周率の信頼区間 ( n = 1000 ) [ 3.135248 3.166827 ]
h = function(x) (cos(50*x)+sin(20*x))^2 n = 10000 x = h(runif(n)) estT = cumsum(x) / (1:n) # 逐次推定量 estE = sqrt(cumsum((x-estT)^2))/(1:n) # 逐次誤差の推定量 plot(estT, type="l", ylim=mean(x)+c(-1,1)*max(estE)/2) lines(estT-2*estE, col="gold") # 信頼区間 lines(estT+2*estE, col="gold") polygon(c(1:n,n:1), c(estT+2*estE,rev(estT-2*estE)), col="wheat") # 色塗り lines(estT)
2項分布の裾確率を重点抽出法を使って推定する。Rの特徴を生かして、配列計算を多用する。
coinTail = function(n=10,n1=8,p=0.7,N=100) {
## 確率pのコインをn回投げる実験をN回(一度に実験して2次元の表にまとめる)
z = matrix(sample(0:1, n*N, prob=c(1-p,p), replace=T),N)
## 表の出た回数(行和)を計算
mm = apply(z,1,sum)
## 尤度を計算
w = ifelse(mm > n1, 1/(2^n * p^mm * (1-p)^(n-mm)), 0)
## 理論値、推定値、推定誤差を計算
c(1-pbinom(n1,n,0.5),mean(w),sd(w)/sqrt(N))
}
## 実行結果の例
> coinTail()
[1] 0.010742188 0.008181948 0.002277226
> coinTail(N=1000)
[1] 0.0107421875 0.0105558658 0.0008391282
M/M/1 モデルでリンドレーの式を使った待ち時間の裾確率推定式を、指数変換法で推定する
### 両側指数分布にしたがう乱数 (S-Aの乱数を生成したい)
rdoubleExp = function(n=20,lmd=0.8,mu=1) {
ww = sample(c(-1,1), n, prob=c(lmd,mu), replace=T)
return(ww * rexp(n) / ifelse(ww==-1,mu,lmd))
}
### リンドレーの式から、ランダムウォークの部分和が閾値を超える確率計算に置き換える
mm1WaitIS = function(lmd=0.8,mu=1,mx = 20,n=100) {
N0 = 1000000
z = rdoubleExp(n=N0)
N = 1
x = numeric(n)
for(i in 1:n) {
## w はランダムウォークの部分和
w = 0
while(w < mx*mu) {
w = w + z[N]
N = N+1
## 用意した乱数系列が尽きたので、新たに生成する
if(N > N0) {z = rdoubleExp(n=N0); N = 1}
}
## w が閾値を超えたときの尤度が独立標本
x[i] = exp(-(mu-lmd)*w)
}
return(c(lmd/mu*exp(-mx*(mu-lmd)),mean(x),sd(x)/sqrt(n))) ## 理論値も計算
}
mm1WaitIS(n=2000,mx=50)
## 実行例 (理論値、推定値、精度)
> mm1WaitIS(n=2000,mx=20)
[1] 1.465251e-02 1.464837e-02 6.681893e-05
> mm1WaitIS(n=2000,mx=30)
[1] 1.983002e-03 1.986179e-03 9.084242e-06
> mm1WaitIS(n=2000,mx=40)
[1] 2.683701e-04 2.685551e-04 1.206908e-06
> mm1WaitIS(n=2000,mx=50)
[1] 3.631994e-05 3.606307e-05 1.709645e-07
(連立)微分方程式系で記述したシステムの時間推移は、その陽解が得られない場合、数値微分で分析することができる。この方法は連続時間シミュレーションとも呼ばれる。
耐久消費財の普及過程を微分方程式で表したものにバスモデルがある。耐久消費財は他の消費者の影響を受けずに製品の魅力で購入するイノベータと呼ばれる人たちと、市場の普及に追随して購入するイミテータと呼ばれる人たちによって普及していくと考える。そうすると、時点 t における普及率を x(t) とすると、x(t) の増分(増加する速度、微分)はイノベータによる貢献部分 p(1-x(t)) とイミテータによる貢献部分 q x(t) (1-x(t)) の和によって表されることになる。ただし、p, q は購入の意欲の強さを表す比例定数である。
x'(t) = (p + q x(t)) (1 - x(t))
数値微分は、微分を微小時間間隔の平均変化率 (x(t+Δt) - x(t)) / Δt に置き換え、t = 0 から順番に x(nΔt) を計算することで実行される。
BassModel = function(p=0.01, q=1, x0=0, dt=0.1, n=100) {
x = rep(x0, n)
for(t in 2:n) x[t] = x[t-1] + (p + q*x[t-1]) * (1 - x[t-1]) * dt
plot(x, type="l")
}
p, q の値をいろいろ変えた場合の普及率の変化のいくつかの例を示す。

インフルエンザなど、人と人との接触によって感染する病気の感染率を表すモデルとして SIR モデルがある。集団を感染候補者Susceptible、感染者Infected、回復者(免疫保持)Recovered の3タイプに分け、その比率の時間変化を微分方程式で表すものである。時刻 t におけるそれぞれのグループの比率を、それぞれの頭文字を取って S(t), I(t), R(t) とする。S(t) + I(t) + R(t) は常に一定であるとして、S(t) は S(t) と I(t) に比例して減少し、R(t) は I(t) に比例して増えると仮定すると、次のような連立微分方程式が成り立つ。ただし、a は感染の強さ、b は治癒力を表す比例定数である。
S'(t) = -a S(t) I(t), I'(t) = a S(t) I(t) - b I(t), R'(t) = b I(t)
バスモデルの場合同様、この3グループの構成率の時間変化は、連立差分方程式に置き換えることで調べることができる。
SIRmodel = function(a=0.1, b=0.03, I0=0.1, dt=0.1, T=100) {
m = floor(T/dt)
S = rep(1, m)
I = rep(I0, m)
R = rep(0, m)
for (t in 2:m) {
S[t] = S[t-1] - dt*a*I[t-1]*S[t-1]
I[t] = I[t-1] + dt*a*I[t-1]*S[t-1] - dt*b*I[t-1]
R[t] = R[t-1] + dt*b*I[t-1]
}
matplot(cbind(S,I,R), type="l")
legend(m/2, 1, c("S","I","R"), lty=1:3, col=1:3, cex=0.8, y.intersp=1.5)
}
.
2国間の戦争の勝敗は戦力の2乗に比例する、というモデル。戦争以外でも、市場のシェア争いのモデルとしても研究されている。
集団間の生存競争、性能が同じならば集団の大きい方が有利
lanchester <- function(a,b,B0,R0,dt,T) {
m = floor(T/dt)
B = rep(B0,m)
R = rep(R0,m)
for (t in 2:m) {
B[t] = B[t-1] - max(0,dt*b*R[t-1])
R[t] = R[t-1] - max(0,dt*a*B[t-1])
}
matplot(cbind(B,R),type="l", ylim=c(0,max(B0,R0)))
}
sup=1.2;
a=0.1;
c=1.2;
X=1000;
lanchester(sup*a, a/c, X, X*c, 0.1, 40)
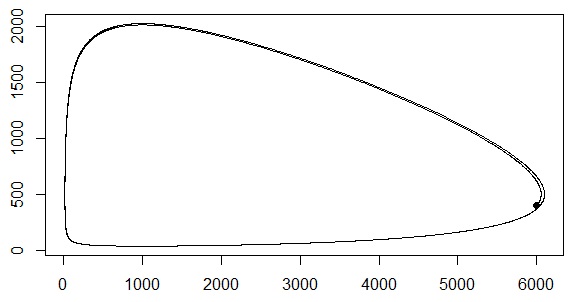
Lotka-Volterraの方程式による生存競争
## Lotka-Volterra の方程式
## dx/dt = x * (a - b * y)
## dy/dt = -y * (c - d * x)
lotkaVolterra = function(a=2,b=0.004,c=1,d=0.001,x0=6000,y0=400,T=10,dt=0.001) {
tmax = T/dt
x = y = numeric(tmax)
x[1] = x0; y[1] = y0
for(t in 2:tmax) {
x[t] = x[t-1] + dt * x[t-1] * (a - b * y[t-1]))
y[t] = y[t-1] - dt * y[t-1] * (c - d * x[t-1]))
}
return(list(x=x,y=y))
}
T = 10; dt = 0.001
v = lotkaVolterra(T=T)
## 時系列グラフ
plot(1:(T/dt), v$x, ylim=c(0,max(v$x)*1.1), type="l")
lines(1:(T/dt), v$y, col=2)
## 散布図
plot(v$x, v$y, type="l")
points(v$x[1], v$y[1], pch=16) # 開始点
サンプル1
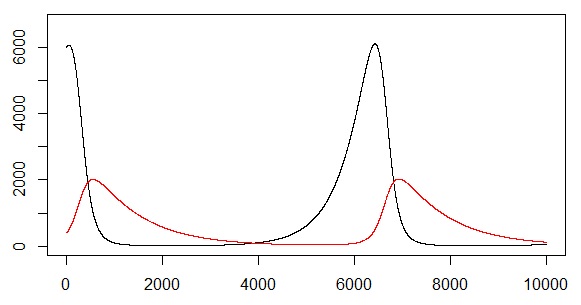
サンプル1