
目次
決められた点から決められた角度で決められた長さ進む、ということを繰り返して曲線(線分の集まり)を描く技法をタートルグラフィックスという。たとえば、ある点からスタートして「1進んで90度右回転する」という動きを4回繰り返すと単位正方形が描ける。
次は、タートルグラフィックスを実現するクラスの例である。
now が現在の座標点、direction が現在の方向を記憶する。方向の単位は「度」とする。setDirection)、方向を変える(turn)、進む(walk)、動く(setPoint)の4つのメソッドが定義されている。class Turtle {
double direction; // 角度、度数表示
Vector2 now; // 現在地
Turtle() {
direction = 0;
now = new Vector2(0, 0);
}
public void reset() {
direction = 0;
now = new Vector2(0, 0);
}
public Vector2 getPoint() {
return now;
}
public double getdirection() {
return direction;
}
// 座標の設定(移動)
public void setPoint(Vector2 z) {
now = z;
}
// 方向の設定(direction の単位はラジアンではなくて「度」)
public void setDirection(double direction) {
this.direction = direction;
}
// 方向転換(theta の単位はラジアンではなくて「度」)
public void turn(double theta) {
direction = mod360(direction + theta);
}
// 指定した距離を移動(方向は変えない)
public void walk(double step) {
now = new Vector2(step*Math.cos(radian(direction)) + now.x,
step*Math.sin(radian(direction)) + now.y);
}
// 度数からラジアンに変換
public double radian(double angle) {
return 2 * Math.PI * angle / 360;
}
// 方向を0度から360度の範囲に収める
double mod360(double angle) {
while (angle < 0) {
angle += 360;
}
while (angle >= 360) {
angle -= 360;
}
return angle;
}
}
class Vector2 {
double x, y;
Vector2(double x, double y) {
this.x = x;
this.y = y;
}
}
例えば、正8角形を描くには、「一定距離進んで45度右回転する」ということを8回繰り返せば良いので、次のようにする。getPoint は現在の座標点を取得するメソッドである。
Turtle t = new Turtle();
t.reset();
Vector2 v = t.getPoint();
for(int i=0; i<8; i++) {
t.walk(1);
// v と t.getPoint() を結ぶ線分を描く
v = t.getPoint();
t.turn(45);
}
}
亀の動線を画面に収めるためには、全部動き終わったあと、その軌跡から範囲を計算して描くしかない。そのために、自動配列 ArrayList データ構造を利用する。
Turtle t = new Turtle();
ArrayList<Vector2> ar = new ArrayList<Vector2>();
t.reset();
ar.add(t.getPoint());
for(int i=0; i<8; i++) {
t.walk(1);
ar.add(t.getPoint()); t.turn(45);
}
draw(ar);
}
// 全部のデータから範囲を計算し、画面に収まるような縮尺率を計算する
void draw(ArrayList<Vector2> r) { Graphics g = getGraphics();
// 範囲を計算
double xa = r.get(0).x, xz = r.get(0).x, ya = r.get(0).y, yz = r.get(0).y; for(int i=1; i<r.size(); i++) { if(r.get(i).x < xa) xa = r.get(i).x;
if(r.get(i).x > xz) xz = r.get(i).x; if(r.get(i).y < ya) ya = r.get(i).y; if(r.get(i).y > yz) yz = r.get(i).y; } double z = Math.max(xz - xa, yz - ya);
// (40,40)- (440,440) の範囲で描画
int ax = 40 + (int)(400 * (r.get(0).x - xa) / z); int ay = 40 + (int)(400 * (r.get(0).y - ya) / z); for(int i=1; i<r.size(); i++) { int bx = 40 + (int)(400 * (r.get(i).x - xa) / z); int by = 40 + (int)(400 * (r.get(i).y - ya) / z); g.drawLine(ax,ay, bx, by); ax = bx; ay = by; } g.dispose(); }
線分を3等分して、真ん中の部分を、それを底辺とする正三角形の2辺で置き換える(下左図)。これを基本図形とし、その図形の各辺(この場合は4つ)を縮小した基本図形で置き換える(下中図)。さらにその図形の各辺(16個ある)を縮小した基本図形で置き換える(下右図)。

この操作を適当な回数繰り返すと、次のような図が得られる。このようにして得られる折れ線をコッホ曲線、繰り返しの回数をその曲線の次数という。
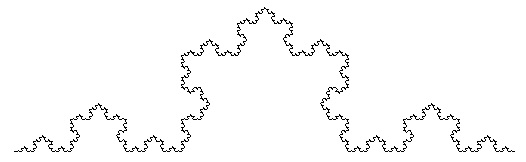
基本図形は次のようにして描くことができる。
各ステップで、一定距離進む(同じ距離を進む)の部分を「基本図形を描く」に置き換えることで、コッホ曲線を描くことが出来る。
次は、上で作成したTurtleクラスのクラスメソッドを使って実現した例である。基本図形の一部を基本図形で置き換えるという操作は、再帰呼び出しを使って実装できる。degree は再帰の回数を表す。
public void Kochsub(int degree, double step) {
if (degree == 0) {
t.walk(step);
// walk の始点と終点を結ぶ線分を描く
} else {
Kochsub(degree - 1, step/3);
t.turn(-60);
Kochsub(degree - 1, step/3);
t.turn(120);
Kochsub(degree - 1, step/3);
t.turn(-60);
Kochsub(degree - 1, step/3);
}
}
あるいは、二つの端点(x1, y1), (x5, y5) を持つ基本図形は3つの折れ線の頂点を指定しても描くことができる。u = (x5 - x1)/3, v = (y5 - y1)/3, t = tan-1((y5 - y1)/(x5 - x1)) として、x2 = x1+ u, y2 = y1 + v; x4 = x1+ 2u, y4 = y1 + 2v; x3 = x1+ (x5 - x1) cos(t+π/6) / cos(t) / √3, y3 = y1+ (y5 - y1) sin(t+π/6) / sin(t) / √3 と置くと、(x1, y1), (x2, y2), (x3, y3), (x4, y4), (x5, y5) を順に結んだものが基本図形になる。
これらの隣接する2点間を直線で結ぶ代わりに基本図形に置き換えると上の真ん中の図のようになる。この手順を繰り返せば、コッホ曲線が描ける。再帰関数で表現すると、例えば次のように表される。
// 再帰関数
public void koch(double x1, double y1, double x5, double y5, int m) {
if(m == 0) {
// 直線 (x1,y1) - (x5,y5) を引く
return;
}
double u = (x5 - x1) / 3;
double v = (y5 - y1) / 3;
double t = Math.atan((y5-y1) / (x5-x1)); double x3 = x1 + (x5-x1) * Math.cos(t+Math.PI/6) / Math.cos(t) / Math.sqrt(3.0);
double y3 = x1 + (y5-y1) * Math.sin(t+Math.PI/6) / Math.sin(t) / Math.sqrt(3.0); koch(x1, y1, x1+u, y1+v, m-1);
koch(x1+u, y1+u, x3, y3, m-1);
koch(x3, y3, x1+2*u, y1+2*v, m-1);
koch(x1+2*u, y1+2*v, x5, y5, m-1);
}
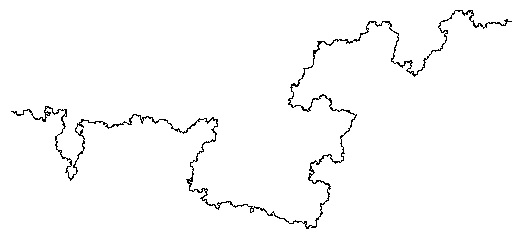
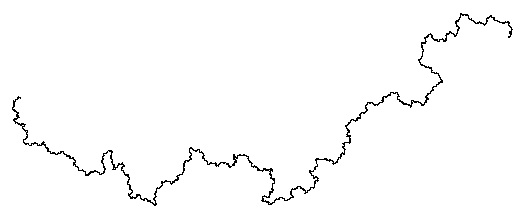
角度や進む距離をランダムにすると、実際の海岸線のような自然界の曲線に近いものが得られる。たとえば、次は0から90までのランダムな数を x, y として、x 度左に、-x-y 度右に、y 度左に方向転換する、と置き換えてコッホ曲線もどきを描いたものである。
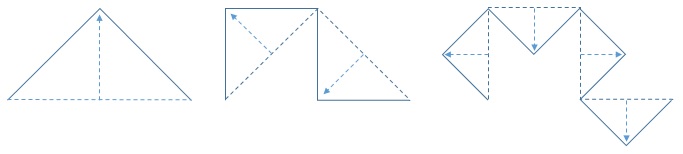
線分の中点をつまんで上に引き上げ、下左図のような直角二等辺三角形の2辺となるようにしたものを基本図形とし、コッホ曲線と同じように、新たに出来た線分を基本曲線で置き換える(ただし、向きが逆)という操作を繰り返してできた折れ線をドラゴン曲線と呼ぶ。
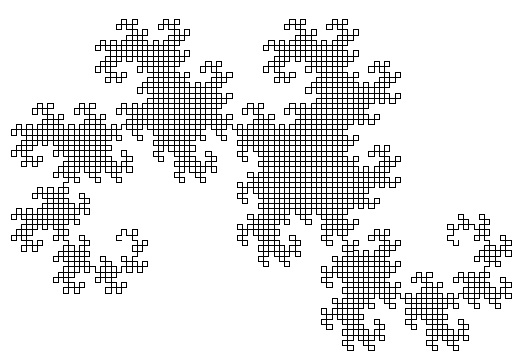
例えば、次はこの操作を12回繰り返した結果得られたものである(12次のドラゴン曲線)。
「ある点から45度左へ向きを変えて、1単位進み、90度右へ向きを変えて1単位進み、45度左に向きを変える」
という動きをI型とし、I型の「右」と「左」を入れ換えた
「ある点から45度右へ向きを変えて、1単位進み、90度左へ向きを変えて1単位進み、45度右に向きを変える」
という動きをII型とする。
I型に続けて「90度右へ向きを変え」てからII型を実行すると上の真ん中の図が描ける。さらに、I型、II型の記述に含まれる最初の「1単位進み」を「I型を実行し」に置き換え、2番目の「1単位進み」を「II型を実行し」に置き換ると、上の右の図が得られる。
上で作成した Turtleクラスのクラスメソッドを使ってこれを実現したのが次のプログラム例である。degree は再帰の回数を表す。
public void dragonsub(int degree, double step, int rot) {
if (degree == 0) {
t.walk(step);
// walk の始点と終点を結ぶ線分を描く
} else {
t.turn(-45*rot);
dragonsub(degree - 1, step/Math.sqrt(2), 1);
t.turn(90*rot);
dragonsub(degree - 1, step/Math.sqrt(2), -1);
t.turn(-45*rot);
}
}
a, b をランダムな数に取り、「45度、90度、45度」の代わりに「a 度、a+b 度、b 度」に置き換えると、次のような自然界に見られる図形のようなものが描ける。
塗りつぶした正三角形から、各片の中点を結んで出来る正三角形の(辺を残して)内部を切り取る。一辺が半分の三つの正三角形それぞれに対して同じ操作を施す、ということを(無限に)繰り返すと、下の図のような穴だらけの三角形ができる。この図形はシェルピンスキーのガスケットと呼ばれる。どんな点の近くでも拡大すると元の図形が出現するという意味で、コッホ曲線と同じような性質を持っている。
これもタートルグラフィックスを使って次のように再帰的に描くことができる。基本図形は正三角形で、「1単位進んで120度左旋回する」ということを3回繰り返す。進む前にその点を左下隅とする大きさが半分のガスケットを描くという作業を追加してやれば良い。

次は、シェルピンスキーのガスケットを描くプログラムの例である。
public void sierpsub(int m, double step) {
if(m == 0) return;
sierpsub(m-1, step/2); // 一辺が半分のガスケットを描く
t.walk(step); // 決められた距離進む
// 歩いた跡の直線を描く
t.turn(-120); // 12度左旋回する、これらをあと2回繰り返す
sierpsub(m-1, step/2);
t.walk(step);
// 歩いた跡の直線を描く
t.turn(-120);
sierpsub(m-1, step/2);
t.walk(step);
// 歩いた跡の直線を描く
t.turn(-120);
}
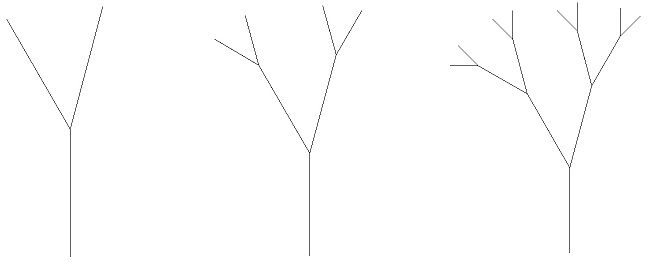
木の枝分かれのような下左図を基本図形とし、その別れた2本の枝を基本図形に置き換えると下中図のようになり、先端の4本の枝を基本図形に置き換えると下右図が得られる。この操作を続けると、木の形をした枝分かれ図がえられる。このような図形を樹形図 tree という。
コッホ曲線を描くのと同様に、タートルグラフィックスを再帰的に使うと、この樹形図が得られる。a, b をそれぞれ左枝、右枝の枝分かれの角度とし、c, d をそれぞれ、幹と枝の長さとすると、基本図形は次のようにして描ける。
c 進み、左へ a 度左旋回して d 進み、枝分かれ地点に戻り、a+b 度右旋回して d 進み、(枝分かれ地点の戻り)b 度左旋回する
「d 進む」ところを基本図形に置き換えると上の中図が得られ、さらにその先端の枝を基本図形に置き換えると上の右図が得られる。次は、枝の長さを再帰の次数とした場合のプログラム例である。a, b をそれぞれ angle, angle2setPoint は現在地を変更するメソッドである。
public void treesub(int degree, double angle, double angle2) {
t.walk(degree);
// ここで枝の始点と終点を結ぶ線を描く
Vector2 v = t.getPoint();
if (degree == 1) {
return;
}
t.turn(-angle);
treesub(degree - 1, angle, angle2);
t.setPoint(v);
t.turn(angle+angle2);
treesub(degree - 1, angle, angle2);
t.setPoint(v);
t.turn(-angle2);
}
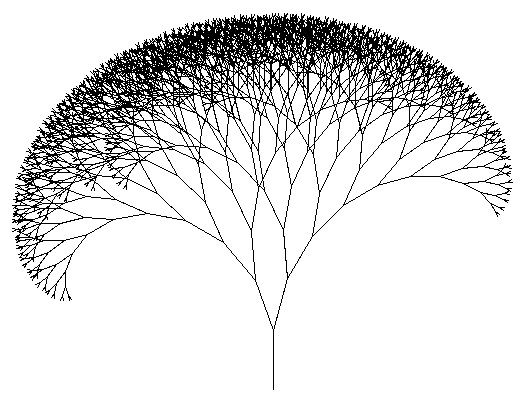
例えば、次は a = 20, b = 15 として、この操作を12回繰り返した結果得られたものである。
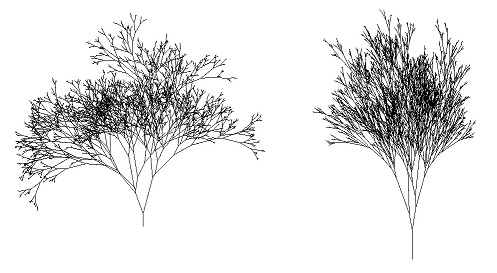
枝の長さをランダムにすると、下のような自然界の木のような図が得られる。
長方形を、その短辺に平行なランダムな直線によって二つの長方形に分ける、という操作を、新たに生成される長方形に対しても適用すると、下図のような図形が出来る。左は4回の操作で24個の長方形に、右は8回の操作で28個の長方形に分割されている。
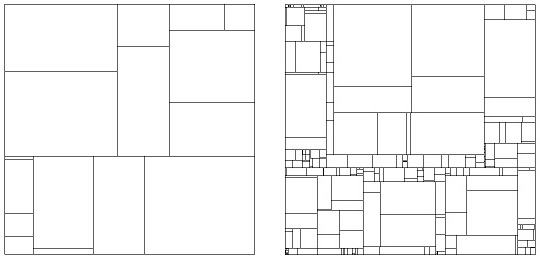
基本操作は次で与えられる。長方形の北西隅の座標を (x1, y1)、南東隅の座標を (x2, y2) とする。
この基本手順を、分割された二つの長方形に適用する、という再帰呼び出しを使えば、上のような図形を描くことが出来る。再帰を終わらせるために、再帰の深さをパラメータとして追加すれば良い。それを実現したのが次のプログラム例である。Vector2 は、2次元の座標点(double型)を表すデータ型である。m は再帰のレベルを記憶する。
// 再帰関数
public void rectsub(Vector2 u, Vector2 w, int m) { if(m == 0) return; if(w.x - u.x > w.y - u.y) { double x = Math.random()*(w.x-u.x) + u.x;
// 点(x, u.y)と点(x, w.y)を結ぶ rectsub(u, new Vector2(x, w.y), m-1); rectsub(new Vector2(x, u.y), w, m-1); } else { double y = Math.random()*(w.y-u.y)+ u.y;
// 点(u.x, y)と点(w.x, y)を結ぶ rectsub(u, new Vector2(w.x, y), m-1); rectsub(new Vector2(u.x, y), w, m-1); } }
c を複素数として、複素数の漸化式「 zn+1 = zn2 + c, z0 = 0」を計算したとき、zn が発散しないような c の全体をマンデルブロ集合という。下左図の黒く塗られた部分がマンデルブロ集合である([-2, 0.5] x [-1, 1] の範囲が示されている)。その一部を拡大したものを真ん中の図、さらにその一部を拡大したものを右図に示す。どんなに拡大しても、同じような図形が現れる。このような性質をフラクタルという。
黒以外の部分では発散するが、その色の違いは、発散の速さに応じて別々の色を配色した結果である。マンデルブロ集合の周辺で拡大した図に細かな色の違いがあるのは、c のちょっとした違いでも、発散のパターンが極端に異なるというフラクタル性があることを示している。
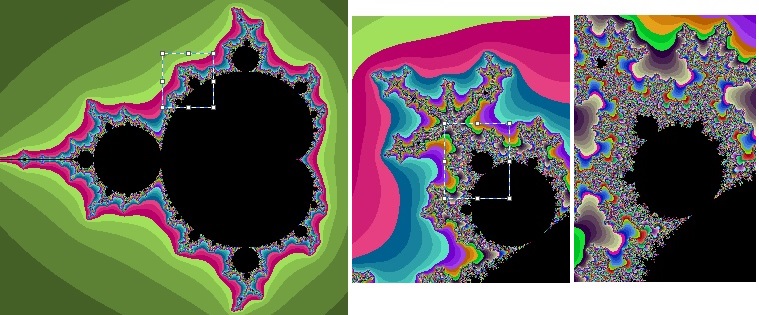
マンデルブロ集合を描くには、適当に大きな値 L と適当に大きな下図 N を与え、複素平面の各点を c として、漸化式を計算し、zN の絶対値が L を超えないものを見つければ良い。ある n で zn が L を超えたら、その n を適当な色コードに変換し、着色する。
次は、そのプログラムの例である。Complex は double型の2次元ベクトルからなるデータ型(複素数を表す)、Complex.add は複素数の足し算、Complex.mult は複素数の掛け算、 Complex.abs2 は複素数の絶対値の2乗を計算する。size はグラフィック領域の大きさを表し、for-(i,j) 文で、各ピクセル毎に複素数を対応させ、漸化式の収束発散を計算している。for-k 構文の if 文で発散したときにループから抜けるようにしている。ループから抜けたときの k の値を r,g,b へ変換する計算方法によって、印象の違う図が得られる。
public void Mandelblotsub(Complex zmin, Complex zmax, int lim, double cov) {
double dx = (zmax.re - zmin.re) / size.width;
double dy = (zmax.im - zmin.im) / size.height;
Complex z, w, c;
for(int i=0; i<size.width; i++) {
for(int j=0; j<size.height; j++) {
c = zmin.add(new Complex(i*dx, j*dy));
z = new Complex(0,0);
int k;
for(k=0; k<lim; k++) {
w = c.add(z.mult(z)); // z = z^2 + c
if(w.abs2() > cov*cov) break;
z = w;
}
int r = (k % 11) * (256/11);
int G = (k % 8) * (256/8);
int b = (k % 19) * (256/19);
if(k == lim) {r = G = b = 0;}
gr.setColor(new Color(r,G,b));
gr.drawOval(i, j, 1, 1);
}
}
repaint();
}
漸化式を適当に替えることにより、マンデルブロ集合と同じようなフラクタル図形を描くことができる。
適当な初期値から始めて、漸化式:xn+1 = a xn + b yn + c; yn+1 = d xn + e yn + f によって点列 {(xn, yn)} を作り出す。例えば、a = d = r cos(t), c = -b = r sin(t), c = f = 0 とすると、回転しながら拡大(r > 1 の場合)、あるいは縮小(r < 1 の場合)していく点列が描かれる。t = 2π/ φ(ただし、φは黄金比(1.618...)), r = 0.999 とすると、下の左の図が得られる。右の図はひまわりの花の写真である。
